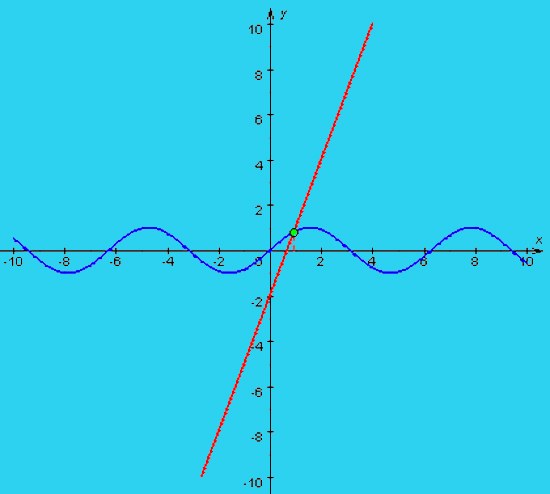
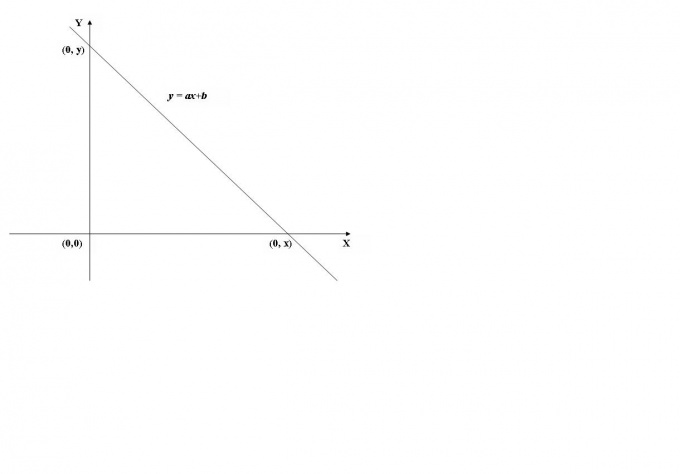
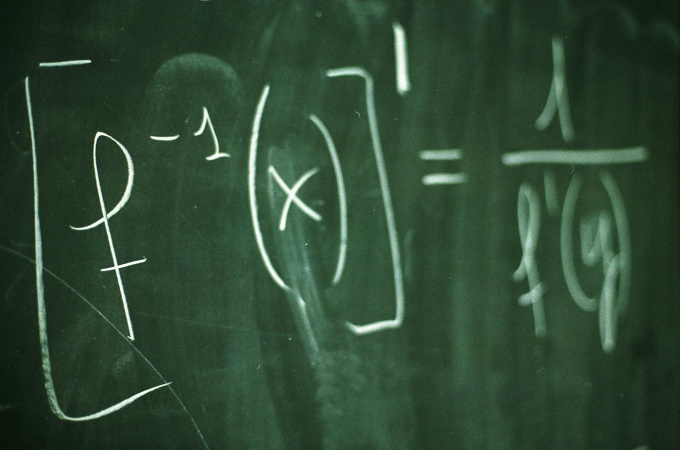Найти абсциссу точки. Друзья! В этой статье для вас размещено ещё несколько заданий связанных с координатной плоскостью. Решение данного типа задач, входящих в состав ЕГЭ очень простенькое – решаются они практически сходу в течение минуты. Если вы забыли, что такое абсцисса и ордината, то посмотрите эту статью .
Суть рассматриваемых ниже задач такая – даны фигуры на плоскости, заданы координаты вершин (не всех), необходимо определить абсциссу или ординату неизвестной вершины. Также имеются задачи на определение длины отрезка. Если у вас развито визуальное (зрительное) представление, то решение вы «увидите» сразу посмотрев на эскиз.
Если есть сложности с визуальным представлением фигур на координатной плоскости, то моя вам «универсальная» рекомендация – постройте фигуру по данным координатам на листе в клетку, далее вы без труда определите координаты (местонахождение) вершины или оговоренной в условии точки и ответите на поставленный вопрос. Посмотрите, как это будет выглядеть такое построение:
Например, абсцисса и ордината точки Р (точка пересечения диагоналей параллелограмма) определяется без труда, соответственно 3 и 4. Рассмотрим задачи:
27673. Точки O (0;0), A (6;8), C (0;6) и B являются вершинами параллелограмма. Найдите ординату точки B.
Точка В смещена относительно точки О в положительном направлении по оси оУ на 2 единицы (также как и точка А смещена относительно точки С), значит её ордината будет равна 0 + 2 = 2.
27674. Точки O (0;0), A (6;8), B (4;2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Ордината точки С равна длине стороны ОС. Известно, что противолежащие стороны параллелограмма равны, то есть ОС = АВ = 8 – 2 = 6.
Точки O (0;0), A (6;8), B (6;2), C (0;6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей.
Обратите внимание на то, что в условии сказано, что дан четырёхугольник, то есть как бы подразумевается, что это возможно это и не параллелограмм.
Но по координатам видно, что это не что иное, как параллелограмм.
*Для убедительности можно построить данную фигуру на координатной плоскости на листе в клетку.
Известно, что точка пересечения диагоналей равноудалена от противолежащих сторон (лежит посередине). Поэтому абсцисса точки Р будет равна 6:2 = 3.
27677. Точки О(0;0), А(10;8), С(2;6) и В являются вершинами параллелограмма. Найдите абсциссу точки В.
Абсцисса точки В на 2 меньше абсциссы точки А (также как абсцисса точки О меньше абсциссы точки С), значит она равна 10 – 2 = 8.
27679 (80). Точки O (0;0), A (10;8), B (8;2) и C являются вершинами параллелограмма. Найдите абсциссу и ординату точки C.
Точка С смещена относительно точки О в положительном направлении по оси оХ на 2 единицы (также как и точка А смещена относительно точки В), значит её абсцисса равна 0 + 2 = 2.
Точка С смещена относительно точки О в положительном направлении по оси оУ на 6 единиц (также как и точка А смещена относительно точки В), значит её ордината равна шести.
Ответ: абсцисса равна 2, ордината равна 6.
27681 (2). Точки O (0;0), B (8;2), C (2;6) и A являются вершинами параллелограмма. Найдите абсциссу и ординату точки A.
Точка А смещена относительно точки С в положительном направлении по оси оХ на 8 единиц (также как и точка В смещена относительно точки О), значит её абсцисса равна 2 + 8 = 10.
Точка А смещена относительно точки В в положительном направлении по оси оУ на 6 единиц (также как и точка С смещена относительно точки О), значит её ордината равна 2 + 6 = 8.
Ответ: Абсцисса точки А равна 10, ордината равна 8.
27683 (4). Точки O (0, 0), A (10, 8), B (8, 2), C (2, 6) являются вершинами четырехугольника. Найдите абсциссу и ординату точки P пересечения его диагоналей.
Можно использовать формулу координат середины отрезка. Формула:
Ответ: абсцисса равна 5, ордината равна 4.
27672. Точки O (0;0), B (6;2), C (0;6) и A являются вершинами параллелограмма. Найдите ординату точки A .
27675. Точки O(0;0), A(6;8), B(6;2), C(0;6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
27678. Точки O(0;0), A(10;8), C(2;6) и B являются вершинами параллелограмма. Найдите ординату точки B.
27685. Точки О(0;0), А(6;8), В(8;2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.
Можно использовать формулу координат середины отрезка, а затем зная их вычислить длину отрезка по соответствующей формуле. Но будет проще и быстрее построить фигуру на координатной плоскости на листе в клетку и вычислить длину отрезка по теореме Пифагора.
27686. Точки O(0;0), A(10;0), B(8;6), C(2;6) являются вершинами трапеции. Найдите длину ее средней линии DE.
Можно использовать формулы координат середины отрезка и затем длины отрезка или построить трапецию н листе в клетку, но в данном случае удобно воспользоваться формулой средней линии трапеции.
источник
Разработать программу на языке С++. Даны вещественные числа x и y . Определить принадлежит ли точка с координатами ( x ; y ) заштрихованной части плоскости. Варианты заданий представлены на рис.3.64 -3.88.
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++.
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++.
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++.
Разработать программу на языке С++ для следующих заданий:
1. Задан круг с центром в точке О ( x 0 , y 0 ), радиусом R 0 и точка А ( x 1 , y 1 ). Определить, находится ли точка внутри круга.
2. Задана окружность с центром в точке О ( x 0 , y 0 ) и радиусом R 0 . Определить пересекается ли заданная окружность с осью абсцисс, если пересекается найти точки пересечения.
3. Задана окружность с центром в точке О ( x 0 , y 0 ) и радиусом R 0 . Определить пересекается ли заданная окружность с осью ординат, если пересекается найти точки пересечения.
Алексеев Е.Р., Чеснокова О.В. Самоучитель по программированию на C/C++.
4. Задана окружность с центром в точке O (0,0) и радиусом R 0 и прямая y = ax + b . Определить, пересекаются ли прямая и окружность. Если пересекаются, найти точки пересечения.
5. Заданы окружности. Первая с центром в точке О ( x 1 , y 1 ) и радиусом R 1 , вторая с центром в точке О ( x 2 , y 2 ) и радиусом R 2. Определить пересекаются окружности, касаются или не пересекаются.
6. Заданы три точки A ( x 1 y 1 ), B ( x 2 , y 2 ), C ( x 3 , y 3 ). Определить какая из точек наиболее удалена от начала координат.
7. Заданы три точки A ( x 1 y 1 ), B ( x 2 , y 2 ), C ( x 3 , y 3 ). Определить какая из точек В или С наименее удалена от точки А .
8. Определить, пересекаются ли линии у=аx +b и у = kx + m . Если пересекаются, найти точку пересечения.
9. Определить, пересекает ли линия у=аx +b ось абсцисс. Если пересекает, найти точку пересечения.
10. Определить, пересекаются ли линии у=аx 3 +bx 2 + сx+d и у = kx + m . Если пересекаются, найти точки пересечения.
11. Определить, пересекаются ли линии у = аx 3 + bx 2 + с x+ d и у = kx 3 + mx 2 + nx + . Если p пересекаются, найти точки пересечения.
12. Определить, пересекаются ли линии у = аx 3 + bx 2 + с x+ d и у = аx 3 + mx 2 + nx + . Если p пересекаются, найти точки пересечения.
13. Определить, пересекаются ли линии у = аx 3 + bx 2 + с x+ d и у = mx 2 + nx + . Если p пересекаются, найти точку пересечения.
14. Определить, пересекает ли линия у = аx 3 + bx 2 + с x+ d ось абсцисс. Если пересекает, найти точку пересечения.
15. Определить, пересекаются ли параболы у = аx 2 + bx + с и у = dx 2 + mx + . Если n пересекаются, то найти точки пересечения.
16. Определить, пересекаются ли линии у = bx 2 + сx + d и у = kx + m . Если пересекаются, найти точки пересечения
17. Найти точки пересечения линии у = аx 2 + bx + с с осью абсцисс. Если линии не пересекаются выдать соответствующее сообщение.
18. Определить, пересекаются ли линии у = аx 4 + bx 3 + сx 2 + dx+f и у = bx 3 + mx 2 + dx + . Если p пересекаются, найти точки пересечения.
19. Определить, пересекаются ли линии у = аx 4 + bx 2 + kx+c и у = mx 2 + kx + . Если p пересекаются, найти точки пересечения.
20. Определить, пересекает ли линия у = аx 4 + bx 2 + c ось абсцисс. Если пересекает, найти точки пересечения.
21. Найти комплексные корни уравнения у = аx 4 + bx 2 + c . Если в уравнении нет комплексных корей вывести соответствующее сообщение.
22. Найти комплексные корни уравнения у=аx 3 +bx 2 + сx+d . Если в уравнении нет комплексных корей вывести соответствующее сообщение.
23. Найти комплексные корни уравнения у=аx 2 +bx+ . с Если в уравнении нет комплексных корей вывести соответствующее сообщение.
24. Даны координаты точки на плоскости. Если точка совпадает с началом координат, то вывести 0. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 1 или 2. Если точка не лежит на координатных осях, то вывести 3.
25. Даны координаты точки, не лежащей на координатных осях OX и OY. Определить номер координатной четверти, в которой находится данная точка.
источник
M (x(t), y(t)) называется точкой самопересечения, если существует такое значение параметра t, что
Чтобы найти точки самопересечения, решим следующую систему уравнений:
(1)
(2)
Разделим уравнение (1) на уравнение (2) почленно:
; нет точек самопересечения.
4. Точки пересечения с осями координат.
А) Найдем точки пересечения γ с осью Оy:
;
;
Итак, точка О (0;0) – точка пересечения γ с Оy.
Б) Найдем точки пересечения γ с осью ox:
;
;
Итак, точка О (0;0) – точка пересечения γ с Ох.
Таким образом, имеем точку пересечения с осями координат:
О (0;0)- точка пересечения γ с Ох и Оу.
5. Поведение на «концах» области определения.
Вычисляем односторонние пределы на концах интервала и (или) пределы на бесконечности. Таким образом, мы исследуем поведение функции на интервале или на бесконечности.
О.О.Ф.: (- ;-1) (-1;1) (1;+ ).
1. Dx(t)= )=(- ;-1) (-1;1) (1; )
2. Dy(t)=(- ;-1) (-1;1) (1; )
источник
Всякий определенный график задается соответствующей функцией. Процесс нахождение точки (нескольких точек) пересечения 2-х графиков сводится к решению уравнения вида f1(x)=f2(x), решение которого и будет являться желанной точкой.
Вам понадобится
1. Еще из школьного курса математики ученикам становится вестимо, что число допустимых точек пересечения 2-х графиков напрямую зависит от вида функций. Так, скажем, линейные функции будут иметь только одну точку пересечения , линейная и квадратная – две, квадратные – две либо четыре, и т.д.
2. Разглядим всеобщий случай с двумя линейными функциями (см. рис.1). Пускай y1=k1x+b1, а y2=k2x+b2. Дабы обнаружить точку их пересечения нужно решить уравнение y1=y2 либо k1x+b1=k2x+b2.Преобразовав равенство, вы получите: k1x-k2x=b2-b1.Выразите x дальнейшим образом:x=(b2-b1)/(k1-k2).
3. Позже нахождения значения х – координаты точки пересечения 2-х графиков по оси абсцисс (ось 0Х), остается вычислить координату по оси ординат (ось 0У). Для этого нужно подставить в всякую из функций, полученное значение х.Таким образом, точка пересечения у1 и у2 будет иметь следующие координаты: ((b2-b1)/(k1-k2);k1(b2-b1)/(k1-k2)+b2).
4. Проанализируйте пример расчета нахождения точки пересечения 2-х графиков (см. рис.2).Нужно обнаружить точку пересечения графиков функций f1 (x)=0,5x^2 и f2 (x)=0,6x+1,2.Приравняв f1 (x) и f2 (x), получите следующее равенство:0,5x^ =0,6x+1,2. Перенеся все слагаемые в левую часть, получите квадратное уравнение вида:0,5x^2 -0,6x-1,2=0.Решением этого уравнения будут два значения х: x1?2,26,x2?-1,06.
5. Подставьте значения х1 и х2 в всякое из выражений функций. Скажем, и f_2 (x1)=0,6•2,26+1,2=2,55, f_2 (x2)=0,6•(-1,06)+1,2=0,56.Выходит, желанными точками являются: т.А (2,26;2,55) и т.В (-1,06;0,56).
График функции y = f (х) – это уйма всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика традиционно выбирается несколько значений довода х и для них вычисляются соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика благотворно обнаружить его точки пересечения с осями координат.
1. Дабы обнаружить точку пересечения графика функции с осью y, нужно вычислить значение функции при х=0, т.е. обнаружить f(0). Для примера воспользуемся графиком линейной функции, изображенной на рис.1. Ее значение при х=0 (y=a*0+b) равно b, следственно, график пересекает ось ординат (ось Y) в точке (0,b).
2. При пересечении оси абсцисс (оси Х) значение функции равно 0, т.е. y=f(x)=0. Для вычисления х нужно решить уравнение f(x)=0. В случае линейной функции получаем уравнение ax+b=0, откуда и находим x=-b/a.Таким образом, ось Х пересекается в точке (-b/a,0).
3. В больше трудных случаях, скажем, в случае квадратичной зависимости y от х, уравнение f(x)=0 имеет два корня, следственно, ось абсцисс пересекается двукратно. В случае периодической зависимости y от х, скажем y=sin(x), ее график имеет безмерное число точек пересечения с осью Х.Для проверки правильности нахождения координат точек пересечения графика функции с осью Х нужно подставить обнаруженные значения х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.
Раньше чем приступить к изысканию поведения функции, нужно определить область метаморфозы рассматриваемых величин. Примем допущение, что переменные относятся к множеству действительных чисел.
1. Функция – это переменная величина, зависящая от значения довода. Довод – переменная самостоятельная. Пределы изменений довода именуются областью возможных значений (ОДЗ). Поведение функции рассматривается в рамках ОДЗ потому, что в этих пределах связанность между двумя переменными не хаотическая, а подчиняется определенным правилам и может быть записана в виде математического выражения.
2. Разглядим произвольную функциональную связанность F=?(x), где ? – математическое выражение. Функция может иметь точки пересечения с осями координат либо с другими функциями.
3. В точках пересечения функции с осью абсцисс функция становится равной нулю:F(x)=0.Решите это уравнение. Вы получите координаты точек пересечения заданной функции с осью ОХ. Таких точек будет столько, сколько найдется корней уравнения на заданном участке метаморфозы довода.
4. В точках пересечения функции с осью ординат значение довода равно нулю. Следственно, задача превращается в нахождение значения функции при х=0. Точек пересечения функции с осью OY будет столько, сколько найдется значений заданной функции при нулевом доводе.
5. Для нахождения точек пересечения заданной функции с иной функцией нужно решить систему уравнений:F=?(x)W=?(x).Тут ?(x) — выражение, описывающее заданную функцию F, ?(x) — выражение, описывающее функцию W, точки пересечения с которой заданной функции необходимо обнаружить. Видимо, что в точках пересечения обе функции принимают равные значения при равных значениях доводов. Всеобщих точек у 2-х функций будет столько, сколько решений у системы уравнений на заданном участке изменений довода.
Видео по теме
В точках пересечения функции имеют равные значения при идентичном значении довода. Обнаружить точки пересечения функций — значит определить координаты всеобщих для пересекающихся функций точек.
1. В всеобщем виде задача нахождения точек пересечения функций одного довода Y=F(x) и Y?=F?(x) на плоскости XOY сводится к решению уравнения Y= Y?, от того что в всеобщей точке функции имеют равные значения. Значения х, удовлетворяющие равенству F(x)=F?(x), (если они существуют) являются абсциссами точек пересечения заданных функций.
2. Если функции заданы несложным математическим выражением и зависят от одного довода х, то задачу нахождения точек пересечения дозволено решить графически. Постройте графики функций. Определите точки пересечения с осями координат (х=0, y=0). Задайте еще несколько значений довода, обнаружьте соответствующие значения функций, добавьте полученные точки на графики. Чем огромнее точек будет использовано для построения, тем вернее будет график.
3. Если графики функций пересекутся, определите по чертежу координаты точек пересечения. Для проверки подставьте эти координаты в формулы, которыми заданы функции. Если математические выражения окажутся объективными, точки пересечения обнаружены положительно. Если графики функций не пересекаются, испробуйте изменить масштаб. Сделайте шаг между точками построения огромнее, дабы определить, на каком участке числовой плоскости линии графиков сближаются. После этого на выявленном участке пересечения постройте больше подробнейший график с мелким шагом для точного определения координат точек пересечения.
4. Если необходимо обнаружить точки пересечения функций не на плоскости, а в трехмерном пространстве, доводится разглядеть функции 2-х переменных: Z=F(x,y) и Z?=F?(x,y). Для определения координат точек пересечения функций надобно решить систему уравнений с двумя незнакомыми х и y при Z= Z?.
источник
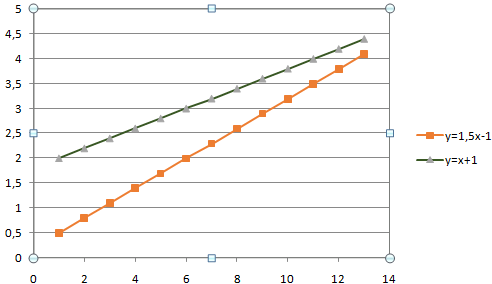
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Существует три показателя, которые измерялись во времени.
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
источник
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квдартичной параболы.В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как ,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена
Дискримнант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:
,
3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем коодинаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подствим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на кординатную плоскость и соединим плавной линией:
2. Уравнение квадратичной функции имеет вид – в этом уравнении – координаты вершины параболы
или в уравнении квадратичной функции , и второй коэффициент – четное число.
Построим для примера график функции .
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно
§ сначала построить график функции ,
§ затем одинаты всех точек графика умножить на 2,
§ затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
§ а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент – четное число.
Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:
(х-2)(х+4)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10113 — 
| 7188 — 
или читать все.
193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
источник
Построение графика произвольной функции может быть как отдельной задачей, так и вспомогательной — например, при решении уравнений графическим способом, или при решении задач с параметрами.
Алгоритм исследования функции 
и построения ее графика таков:
1. Находим область определения (D(f)) функции .
2. Если область определения функции симметрична относительно нуля (то есть для любого значения 
из D(f) значение 
также принадлежит области определения, то проверяем функцию на четность.
Если 
, то функция четная . (Примером четной функции является функция 
)
Для нас важно, что график четной функции симметричен относительно оси OY.
Если 
, то функция нечетная . (Примером нечетной функции является функция 
)
График нечетной функции симметричен относительно начала координат.
Если функция является четной или нечетной, то мы можем построить часть ее графика для 
=0″ title=»x>=0″/>
, а затем соответствующим образом отразить ее.
3. Находим точки пересечения графика с осями координат.
Находим нули функции — это точки пересечения графика функции с осью абсцисс (OX).
Для этого мы решаем уравнение 
.
Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ.
Находим точку пересечения графика функции с осью ординат (OY). Для этого ищем значение функции при 
.
4. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции , нам нужно решить неравенства 
0″ title=»f(x)>0″/> и 
.
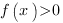
5. Находим асимптоты графика функции.
Краткий экскурс на тему, что такое асимптоты и как их находить читайте здесь.
6. Если функция периодическая, то находим период функции.
7. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную 
б) Приравниваем производную к нулю и находим корни уравнения 
— это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
8. И последний номер наше программы — точки перегибы и промежутки выпуклости и вогнутости.
Подробнее о том, как находить точки перегиба и промежутки выпуклости и вогнутости читайте здесь.
Итак, давайте, для примера, исследуем функцию 
и построим ее график.
1. Найдем D(y).
0″ title=»
Сразу отметим, что при 
знаменатель дроби равен нулю, следовательно, прямые 
и 
являются вертикальными асимптотами графика функции .
2. Исследуем функцию на четность. Область определения функции симметрична относительна нуля (мы выкололи две симметричные точки: и )
Получили, что , следовательно, функция — нечетная, и график функции симметричен относительно начала координат.
3. Найдем точки пересечения с осями координат.
а) Точки пересечения с осью ОХ (y=0)
б) Точка пересечения с осью ОY (x=0)
График нашей функции проходит через начало координат.
4. Найдем промежутки знакопостоянства.
Решим неравенство 
0″ title=»
Найдем корни числителя и знаменателя, нанесем их на числовую ось и расставим знаки:
Корень числителя:
Корни знаменателя: ;
Итак, 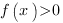0″ title=»f(x)>0″/> при 
и 
при 
и 
5. Найдем асимптоты графика функции .
Вертикальные асимптоты мы уже нашли в п.1, это прямые и .
Уравнение горизонтальной асимптоты функции имеет вид 
, где
.
Степень числителя дроби 
на единицу больше степени знаменателя, поэтому 
не существует, и график функции не имеет горизонтальной асимптоты.
Попробуем найти наклонную асимптоту.
Уравнение наклонной асимптоты имеет вид 
.
Коэффициенты 
и 
вычисляются следующим образом:
В нашем случае 
.
(Степень знаменателя на единицу больше степени числителя).
То есть уравнение наклонной асимптоты имеет вид 
.
Нанесем асимптоты на координатную плоскость:
6. Найдем промежутки возрастания-убывания функции и экстремумы.
а) Найдем производную функции
б) Приравняем производную к нулю:
(корень четной кратности); 
; 
Корни знаменателя — — также корни четной кратности.
В корнях четной кратности производная знак не меняет.
в) Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания.
Итак, мы нашли промежутки возрастания и убывания.
Найдем значение функции в точках экстремума:
Заметим, что, поскольку функция нечетная, и мы нашли, что 
, мы могли бы сразу написать, что 
Итак, отметим в нашей координатной плоскости точки минимума и максимума функции и точку пересечения графика функции с осями координат.
На рисунке ниже большими красными кружками обозначены точки, через которые проходит график функции.
Теперь учтем промежутки возрастания-убывания и промежутки знакопостоянства функции (п. 4) и построим ее график. Помним, что график функции не пересекает абсциссы, он лишь приближается к ним!
После построения графика необходимо еще раз просмотреть все пункты исследования функции и проверить, соответствует ли полученный график всем пунктам.
Если наблюдается какое-то несоответствие, то необходимо повторить исследование и найти причину нестыковки графика и поведения функции.
источник
Даны два отрезка, каждый из которых задан двумя точками: (v11, v12), (v21, v22). Необходимо определить, пересекаются ли они, и если пересекаются, найти точку их пересечения.
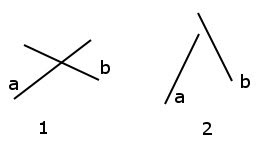
Для начала необходимо определить, пересекаются ли отрезки. Необходимое и достаточное условие пересечения, которое должно быть соблюдено для обоих отрезков следующее: конечные точки одного из отрезков должны лежать в разных полуплоскостях, если разделить плоскость линией, на которой лежит второй из отрезков. Продемонстрируем это рисунком. 
На левом рисунке (1) показаны два отрезка, для обоих из которых условие соблюдено, и отрезки пересекаются. На правом (2) рисунке условие соблюдено для отрезка b, но для отрезка a оно не соблюдается, соответственно отрезки не пересекаются.
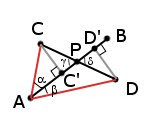
Может показаться, что определить, с какой стороны от линии лежит точка — нетривиальная задача, но у страха глаза велики, и всё не так сложно. Мы знаем, что векторное умножение двух векторов даёт нам третий вектор, направление которого зависит от того, положительный или отрицательный угол между первым и вторым вектором, соответственно такая операция антикоммутативна. А так как все вектора лежат на плоскости X-Y, то их векторное произведение (которое обязано быть перпендикулярным перемножаемым векторам) будет иметь ненулевой только компоненту Z, соответственно и отличие произведений векторов будет только в этой компоненте. Причем при изменении порядка перемножения векторов (читай: угла между перемножаемыми векторами) состоять оно будет исключительно в изменении знака этой компоненты.
Поэтому мы можем умножить попарно-векторно вектор разделяющего отрезка на векторы направленные от начала разделяющего отрезка к обеим точкам проверяемого отрезка. 
Если компоненты Z обоих произведений будет иметь различный знак, значит один из углов меньше 0 но больше -180, а второй больше 0 и меньше 180, соответственно точки лежат по разные стороны от прямой. Если компоненты Z обоих произведений имеют одинаковый знак, следовательно и лежат они по одну сторону от прямой.
Если один из компонент Z является нулём, значит мы имеем пограничный случай, когда точка лежит аккурат на проверяемой прямой. Оставим пользователю определять, хочет ли он считать это пересечением.
Затем нам необходимо повторить операцию для другого отрезка и прямой, и убедиться в том, что расположение его конечных точек также удовлетворяет условию.
Итак, если всё хорошо и оба отрезка удовлетворяют условию, значит пересечение существует. Давайте найдём его, и в этом нам также поможет векторное произведение.
Так как в векторном произведении мы имеем ненулевой лишь компоненту Z, то его модуль (длина вектора) будет численно равен именно этой компоненте. Давайте посмотрим, как найти точку пересечения. 
Длина векторного произведения векторов a и b (как мы выяснили, численно равная его компоненте Z) равна произведению модулей этих векторов на синус угла между ними (|a| |b| sin(ab)). Соответственно, для конфигурации на рисунке мы имеем следующее: |AB x AC| = |AB||AC|sin(α), и |AB x AD| = |AB||AD| sin(β). |AC|sin(α) является перпендикуляром, опущенным из точки C на отрезок AB, а |AD|sin(β) является перпендикуляром, опущенным из точки D на отрезок AB (катетом ADD’). Так как углы γ и δ — вертикальные углы, то они равны, а значит треугольники PCC’ и PDD’ подобны, а соответственно и длины всех их сторон пропорциональны в равном отношении.
Имея Z1 (AB x AC, а значит |AB||AC|sin(α) ) и Z2 (AB x AD, а значит |AB||AD|sin(β) ), мы можем рассчитать CC’/DD’ (которая будет равна Z1/Z2), а также зная что CC’/DD’ = CP/DP легко можно высчитать местоположение точки P. Лично я делаю это следующим образом:
Px = Cx + (Dx-Cx)*|Z1|/|Z2-Z1|;
Py = Cy + (Dy-Cy)*|Z1|/|Z2-Z1|;
Вот и все. Мне кажется что это действительно очень просто, и элегантно. В заключение хочу привести код функции, реализующий данный алгоритм. В функции использован самодельный шаблон vector , который является шаблоном вектора размерностью int с компонентами типа typename. Желающие легко могут подогнать функцию к своим типам векторов.
Редакторы Хабра врываются в велосезон, каждый по-своему
источник
Для построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Например, трудно вычертить вид сверху детали, приведенной на рис. 139, не строя горизонтальных проекций точек А, В, С, D, Е, F и др.
Рис. 139. Деталь, для построения вида сверху которой необходимо найти проекции точек
Задача нахождения проекций точек по одной, заданной на поверхности предмета, решается следующим образом. Сначала находят проекции поверхности, на которой расположена точка. Затем, проведя линию связи к проекции, где поверхность изображается линией, находят вторую проекцию точки. Третья проекция лежит на пересечении линий связи.
Даны три проекции детали (рис. 140, а). Задана горизонтальная проекция а точки А, лежащей на видимой поверхности. Нужно найти остальные проекции этой точки.
Рис. 140. Построение проекций точек, заданных на поверхности предмета
Прежде всего надо провести вспомогательную прямую. Если даны два вида, то место вспомогательной прямой на чертеже выбирают произвольно, правее вида сверху, так чтобы вид слева оказался на нужном расстоянии от главного вида (рис. 141).
Рис. 141. Расположение третьего вида определяется местом вспомогательной прямой
Если три вида уже построены (рис. 142, а), то место вспомогательной прямой произвольно выбирать нельзя; нужно найти точку, через которую она пройдет. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии и через полученную точку k (рис. 142, б) провести под углом 45° отрезок прямой, который и будет вспомогательной прямой.
Если осей симметрии нет, то продолжают до пересечения в точке k1 горизонтальную и профильную проекции любой грани, проецирующейся в виде отрезков прямой (рис. 142, б).
Рис. 142. Построение вспомогательной прямой
Проведя вспомогательную прямую, приступают к построению проекций точки (см. рис. 140, б).
Фронтальная а’ и профильная а» проекции точки А должны располагаться на соответствующих проекциях поверхности, которой принадлежит точка А. Находят эти проекции. На рис. 140, б они выделены цветом. Проводят линии связи, как указано стрелками. В местах пересечения линий связи с проекциями поверхности находятся искомые проекции а’ и а».
Построение проекций точек В, С, D показано на рис. 140, в линиями связи со стрелками. Заданные проекции точек цветные. Линии связи проводят к той проекции, на которой поверхность изображается в виде линии, а не в виде фигуры. Поэтому сначала находят фронтальную проекцию с’ точки С. Профильная проекция с точки С определяется пересечением линий связи.
Если поверхность ни на одной проекции не изображается линией, то для построения проекций точек надо применять вспомогательную плоскость. Например, дана фронтальная проекция d точки А, лежащей на поверхности конуса (рис. 143, а). Через точку параллельно основанию проводят вспомогательную плоскость, которая пересечет конус по окружности; ее фронтальная проекция — отрезок прямой, а горизонтальная — окружность диаметром, равным длине этого отрезка (рис. 143, б). Проведя к этой окружности из точки а’ линию связи, получают горизонтальную проекцию а точки А.
Рис. 143. Построение проекций точки, заданной на поверхности конуса
Профильную проекцию а» точки А находят обычным способом на пересечении линий связи.
Таким же приемом можно найти проекции точки, лежащей, например, на поверхности пирамиды или шара. При пересечении пирамиды плоскостью, параллельной основанию и проходящей через заданную точку, образуется фигура, подобная основанию. На проекциях этой фигуры лежат проекции заданной точки.
1. Под каким углом проводят вспомогательную прямую?
2. Где проводят вспомогательную прямую, если заданы виды спереди и сверху, а надо построить вид слева?
3. Как определить место вспомогательной прямой при наличии трех видов?
4. В чем заключается способ построения проекций точки по одной заданной, если одна из поверхностей предмета изображается линией?
5. Для каких геометрических тел и в каких случаях проекции точки, заданной на их поверхности, находят, пользуясь вспомогательной плоскостью?
Запишите в рабочей тетради, каким проекциям точек, обозначенных на видах цифрами, соответствуют точки, обозначенные на наглядном изображении буквами в примере, указанном Вам преподавателем (рис. 144, а-г).
Форма записи:
Рис. 144. Задания на определения положения точек
На рис. 145, а-б буквами обозначено лишь по одной проекции некоторых из вершин. Найдите в примере, указанном Вам преподавателем, остальные проекции этих вершин и обозначьте их буквами. Постройте в одном из примеров недостающие проекции точек, заданных на ребрах предмета (рис. 145, г и д). Выделите цветом проекции ребер, на» которых находятся точки. Задание выполните на прозрачной бумаге, наложив ее на страницу учебника. Перечерчивать рис. 145 не надо.
Рис. 145. Задания на обозначение проекций вершин и нахождение проекций точек
Найдите недостающие проекции точек, заданных одной проекцией на видимых поверхностях предмета (рис. 146). Обозначьте их буквами. Заданные проекции точек выделите цветом. Решить задание Вам поможет наглядное изображение. Задание можно выполнить как в рабочей тетради, так и на прозрачной бумаге, наложив ее на страницу учебника. В последнем случае перечерчивать рис. 146 не надо.
Рис. 146. Задания на построение недостающих проекций точек
В примере, указанном Вам преподавателем, перечертите три вида (рис. 147). Постройте недостающие проекции точек, заданных на видимых поверхностях предмета. Заданные проекции точек выделите цветом. Обозначьте буквами все проекции точек. Для построения проекций точек воспользуйтесь вспомогательной прямой. Выполните технический рисунок и нанесите на нем заданные точки.
Рис. 147. Задания на построение недостающих проекций точек и выполнение технических рисунков
Перечертите два вида (рис. 148), постройте третий. Найдите недостающие проекции точек. Заданные проекции точек выделите цветом. Обозначьте буквами все проекции точек. Линии построений не стирайте.
Рис. 148. Задания на построение третьего вида и недостающих проекций точек
В чертежах на рис. 149 допущены ошибки — отсутствуют некоторые линии (видимого и невидимого контуров, а также осевые). Исправьте допущенные ошибки, для чего перечертите заданные изображения и дочертите пропущенные линии. Выделите эти линии цветом. Задание можно выполнить на прозрачной бумаге, наложив ее на рис. 149. Выполните технические рисунки деталей, из чертежа которых Вы дочерчивали линии.
Рис. 149. Задания на дочерчивание недостающих линий
источник